import matplotlib.pyplot as plt
import numpy as np
X_train=np.arange(10).reshape((10, 1))
y_train=np.array([1.0, 1.3, 3.1, 2.0, 5.0, 6.3, 6.6, 7.4, 8.0, 9.0])
plt.plot(X_train, y_train, 'o', markersize=10)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
import tensorflow as tf
X_train_norm=(X_train-np.mean(X_train))/np.std(X_train)
ds_train_orig=tf.data.Dataset.from_tensor_slices((tf.cast(X_train_norm, tf.float32), tf.cast(y_train, tf.float32)))
선형 회귀 모델 정의
class MyModel(tf.keras.Model):
def __init__(self):
super(MyModel, self).__init__()
self.w=tf.Variable(0.0, name='weight')
self.b=tf.Variable(0.0, name='bias')
def call(self, x):
return self.w*x+self.b
모델 객체 생성
model=MyModel()
model.build(input_shape=(None, 1))
model.summary()
Model: "my_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________
차원의 크기(기대하는 크기)를 None으로 지정하면, 임의의 배치 크기를 사용
하지만 특성 개수는 모델의 가중치 파라미터의 개수와 직접적으로 연관이 있음
입력(nXm), W_in(mXd), o_in(nXd)
pi(o_in)(nXd), W_out(dXl), O(nXl)
특성개수: m 모델의 가중치(mXd)와 관련 있다. 따라서 특성 개수는 고정적이다.
위와 같이 객체를 생성( model=MyModel() ) 후, .build() 메서드를 호출하여 모델 층과 파라미터를 만드는 방법을
변수 지연 생성(late variable creation)라고 한다.
비용함수를 지정할 수 있다. 아래는 평균 제곱 오차(Mean Squared Error, MSE)를 비용함수로,
모델의 가중치 파라미터를 학습시키기 위해 확률적 경사 하강법을 사용한다.
아래에서는 직접 확률적 경사 하강법 훈련 과정을 구현하지만, 케라스에서 compile()과 fit() 메서드를 사용할 수 있다.
def loss_fn(y_true, y_pred):
return tf.reduce_mean(tf.square(y_true-y_pred))
def train(model, inputs, outputs, learning_rate):
with tf.GradientTape() as tape:
current_loss=loss_fn(model(inputs), outputs)
dW, db=tape.gradient(current_loss, [model.w, model.b])
model.w.assign_sub(learning_rate*dW)
model.b.assign_sub(learning_rate*db)
200번의 에포크 동안 훈련배치를 만들고 count=None으로 데이터셋을 반복(무한히 반복한다.)
tf.random.set_seed(1)
num_epochs=200
log_steps=100
learning_rate=0.001
batch_size=1
steps_per_epoch=int(np.ceil(len(y_train)/batch_size))
ds_train=ds_train_orig.shuffle(buffer_size=len(y_train))
ds_train=ds_train.repeat(count=None)
ds_train=ds_train.batch(1)
Ws, bs=[], []
for i, batch in enumerate(ds_train):
if i>=steps_per_epoch*num_epochs:
break
Ws.append(model.w.numpy())
bs.append(model.b.numpy())
bx, by=batch
loss_val=loss_fn(model(bx), by)
train(model, bx, by, learning_rate=learning_rate)
if i%log_steps==0:
print('epochs {:3d} steps {:4d} loss {:6.4f}'.format(int(i/steps_per_epoch), i, loss_val))
epochs 0 steps 0 loss 43.5600
epochs 10 steps 100 loss 0.7530
epochs 20 steps 200 loss 20.1759
epochs 30 steps 300 loss 23.3976
epochs 40 steps 400 loss 6.3481
epochs 50 steps 500 loss 4.6356
epochs 60 steps 600 loss 0.2411
epochs 70 steps 700 loss 0.2036
epochs 80 steps 800 loss 3.8177
epochs 90 steps 900 loss 0.9416
epochs 100 steps 1000 loss 0.7035
epochs 110 steps 1100 loss 0.0348
epochs 120 steps 1200 loss 0.5404
epochs 130 steps 1300 loss 0.1170
epochs 140 steps 1400 loss 0.1195
epochs 150 steps 1500 loss 0.0944
epochs 160 steps 1600 loss 0.4670
epochs 170 steps 1700 loss 2.0695
epochs 180 steps 1800 loss 0.0020
epochs 190 steps 1900 loss 0.3612
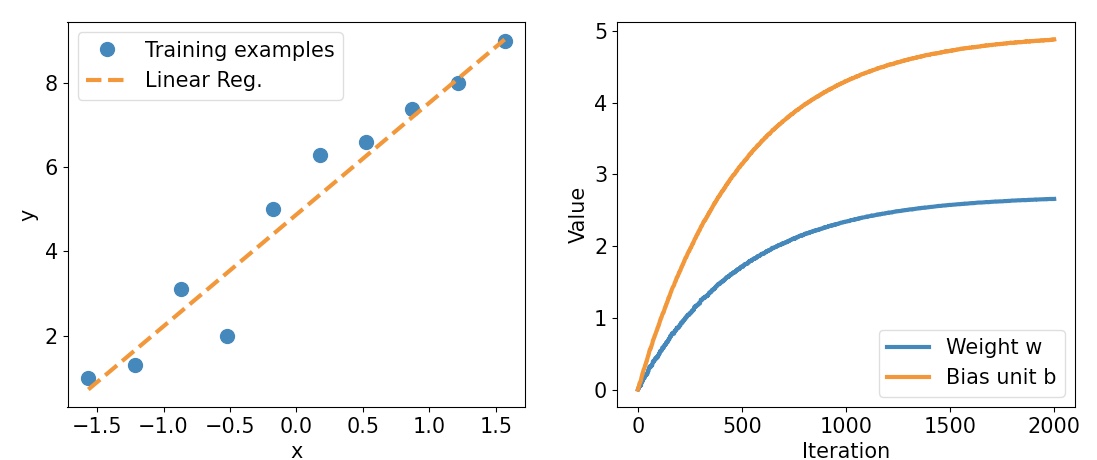
print('최종 파라미터: ',model.w.numpy(), model.b.numpy())
최종 파라미터: 2.6576622 4.8798566
X_test=np.linspace(0, 9, num=100).reshape(-1, 1)
X_test_norm=(X_test-np.mean(X_train))/np.std(X_train)
y_pred=model(tf.cast(X_test_norm, dtype=tf.float32))
fig=plt.figure(figsize=(13, 5))
ax=fig.add_subplot(1, 2, 1)
plt.plot(X_train_norm, y_train, 'o', markersize=10)
plt.plot(X_test_norm, y_pred, '--', lw=3)
plt.legend(['Training examples', 'Linear Reg.'], fontsize=15)
ax.set_xlabel('x', size=15)
ax.set_ylabel('y', size=15)
ax.tick_params(axis='both', which='major', labelsize=15)
ax=fig.add_subplot(1, 2, 2)
plt.plot(Ws, lw=3)
plt.plot(bs, lw=3)
plt.legend(['Weight w', 'Bias unit b'], fontsize=15)
ax.set_xlabel('Iteration', size=15)
ax.set_ylabel('Value', size=15)
ax.tick_params(axis='both', which='major', labelsize=15)
plt.show()
using .compile(), .fit()
케라스의 compile, fit 메서드를 이용하면, 위처럼 train 함수를 만들지 않아도 된다.
새로운 모델을 만든 후, 옵티마이저(optimizer), 손실 함수, 평가 지표
fit 메서드는 위에서 처럼 ds_train과 같은 배치 데이터셋을 전달
데이터셋이 아닌 X, y 전달도 가능
tf.random.set_seed(1)
model=MyModel()
model.compile(optimizer='sgd', loss=loss_fn, metrics=['mae', 'mse'])
model.fit(X_train_norm, y_train, epochs=num_epochs, batch_size=batch_size, verbose=1)
…(생략)
Epoch 196/200
10/10 [==============================] - 0s 267us/step - loss: 0.4426 - mae: 0.5243 - mse: 0.4426
Epoch 197/200
10/10 [==============================] - 0s 256us/step - loss: 0.3621 - mae: 0.4244 - mse: 0.3621
Epoch 198/200
10/10 [==============================] - 0s 255us/step - loss: 0.2078 - mae: 0.3295 - mse: 0.2078
Epoch 199/200
10/10 [==============================] - 0s 264us/step - loss: 0.3584 - mae: 0.4830 - mse: 0.3584
Epoch 200/200
10/10 [==============================] - 0s 258us/step - loss: 0.2087 - mae: 0.3927 - mse: 0.2087
<tensorflow.python.keras.callbacks.History object at 0x176e628e0>